For years, I wanted to learn machine learning, but one thing always held me back: my intense fear of mathematical equations. I had started multiple times, but the moment those terrifying equations appeared, it was an immediate turn-off. As much as I feared math, the beauty of machine learning kept pulling me back. Eventually, the fear of missing out became stronger than the fear of math, and I decided it was finally time to face the monster.
Like most machine learning warriors I know, I started with Andrew Ng's Machine Learning Specialization. I dived into the course, fully prepared for battle. Everything was going smoothly… until the first boss appeared.

How do you fight a level 100+ boss when you're only level 10? From my previous failed expeditions, I had learned one thing: never blindly attack an enemy. First, learn about its powers. Then, level up to match them. That's what a sane warrior would do. And that's exactly what I tried to do.
If you find yourself in this situation, this guide is for you. This is the story of a noob warrior named Peter.
Our warrior Peter explored the land, searching for information about the dragon Lingressithrax. At the foot of the mountain, he reached a village and met an old warrior. He told Peter that he had once tried to fight the dragon — but had failed. He couldn't even leave a small scratch on it. Yet, he hadn't returned empty-handed. During the battle, he had carefully observed something important: the intensity of the dragon's fire at various distances from the beast itself.

He shared these observations with Peter.
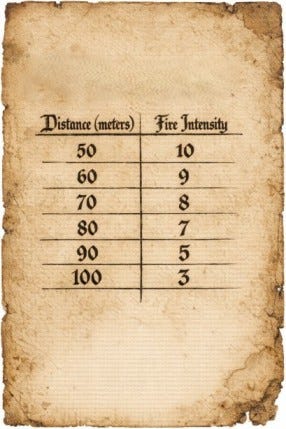
With no other information available, Peter decided he would have to gather details about the dragon himself. To do that, he needed to get closer. Using the small amount of knowledge he had gained from the old warrior, Peter began formulating a plan. He imagined creating a spell — one that could reveal how intense the dragon's fire would be at any given distance. Such a spell would help him decide whether to advance or abort the mission altogether. He figured this spell would come in handy. But first, he would need a staff.

Peter first decided that he should visualize the data. So, he created a graph.
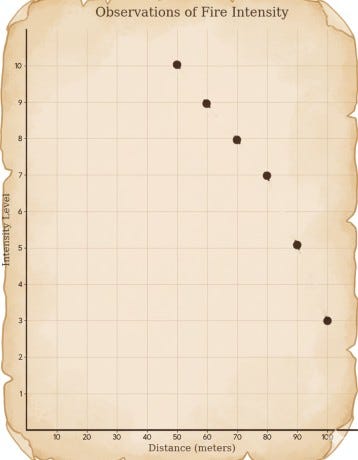
He noticed that the points looked somewhat linear.
He noticed that the points appeared to form a roughly straight line. This gave him an idea: if he could draw a straight line through the points, then for any given distance from the dragon, he could simply move vertically up to the line and estimate the intensity of the fire he might expect.
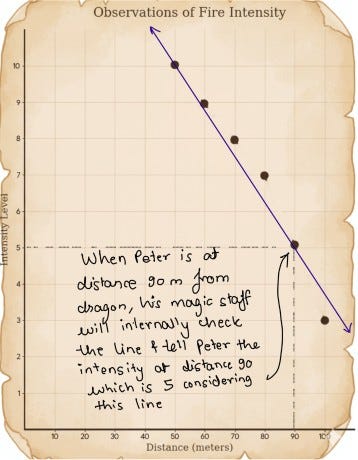
"Great idea!" Peter thought.
But loading this spell into his mage staff wasn't so simple. He couldn't just show the staff a piece of paper with a drawn line and expect it to understand. The staff required the spell to be described in its own language.
To do that, Peter had to craft the spell using the tools he had. And now a new problem arose: how could he describe a line in a language his staff would understand?
Peter drew a straight line on the graph and began studying it. For a long time, he simply stared at the paper. Then, something interesting caught his eye. He started jotting down his observations.
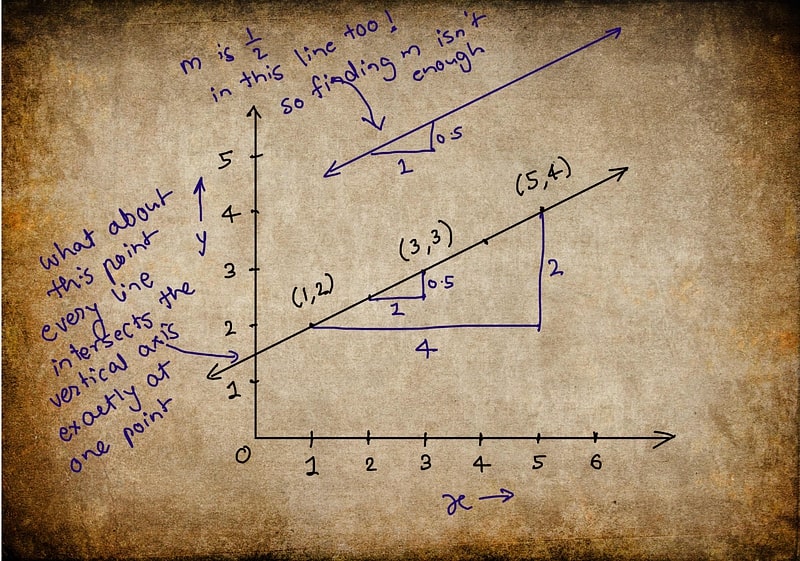
His first observation was about how the line behaved as he moved along it.
Every time he moved a little to the right on the graph (a change in x), the value of y also changed. And it didn't change randomly — the change was proportional.
Δy ∝ Δx
Curious, Peter looked at the ratio between these two changes. No matter which two points on the line he chose, this ratio stayed the same.
He decided to give this ratio a name. He called it m.
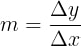
This value told Peter how steep the line was — how quickly the fire intensity changed as he moved closer or farther away.
To make this more concrete, Peter picked two points on the line.
He chose the point (1, 2) and called it (x₁, y₁).
He then chose another point, (5, 4), and called it (x₂, y₂).
To find the value of m, he looked at how much y changed compared to how much x changed between these two points.
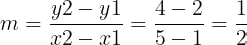
No matter which two points Peter chose on the line, this ratio always came out the same.
But m only told Peter how y changed with respect to x.
What he actually wanted was something more practical — given a distance from the dragon (x), he wanted to directly estimate the fire intensity (y).
As he looked at the graph, Peter realized that m was simply describing the slope of the line — how steep it was.
But slope alone wasn't enough.
There could be infinitely many lines with the same slope, all parallel to each other. Yet only one of them matched his observations.
So Peter asked himself, "What is missing? What distinguishes this line from all the others?"
Looking carefully at the graph, Peter noticed something important.
Every straight line — except a vertical one — crosses the y-axis at exactly one point. And no two distinct lines with the same slope can share the same y-intercept.
That was it.
This point of intersection was the missing piece.
Together, the slope and this intercept uniquely defined the line.
Peter decided to anchor the line using its y-intercept.
He took the point where the line crossed the y-axis, (0, 1.5), and called it (x₁, y₁).
Next, he chose a distance x₂ = 3, where he wanted to find the corresponding fire intensity y₂
Using the same idea as before, he wrote:
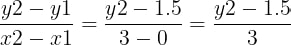
But he already knew that this ratio was simply the slope, m. So he wrote:
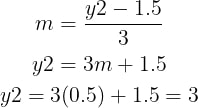
At a distance of x = 3, the equation predicted a fire intensity of y = 3.
At x = 5, the same rule — 5m + 1.5 — gave y = 4.
And this worked for any distance. The same simple rule worked everywhere along the line.
So, for Peter's line, he could now find the value of y for any given x using the equation:
y=mx+1.5
To make this spell more general, Peter decided to give the y-intercept a letter. He called it c.
With that, the equation became:
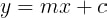
Perfect.
He had finally described a line in a language his staff could understand.
Now that Peter knew how to load any line into his staff, all that remained was to draw one through the fire-intensity points on the graph. He could then calculate its slope m and y-intercept c, feed those values into the staff, and let the spell do its work. For any distance x— how far Peter stood from the dragon — the staff would tell him the fire intensity to expect.
Confident, Peter turned back to the graph and began drawing the line. That's when he encountered a small, unexpected problem: the points weren't perfectly colinear. How, then, could he draw the "right" line?
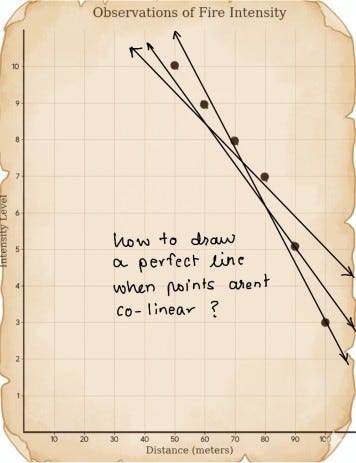
Peter could have just drawn a line and left it at that. But he wanted his spell to be as accurate as possible — after all, he already had so little information about the dragon.
So he paused and thought:

To start, Peter drew three different lines through the points.
Then he asked himself, "Is there a way to measure which line is more accurate?"
Suddenly, an idea popped into his mind. Each line gave a prediction — for any distance x, the y-coordinate of the line estimated the dragon's fire intensity. And Peter already had the actual fire intensities for each distance — his data points.
"What if I subtract the predicted fire intensity from the actual fire intensity at each point?", he thought.
He could do this for all the points he had and then combine all these differences — all the 'errors'. Then he could pick the line for which the total error was the smallest.
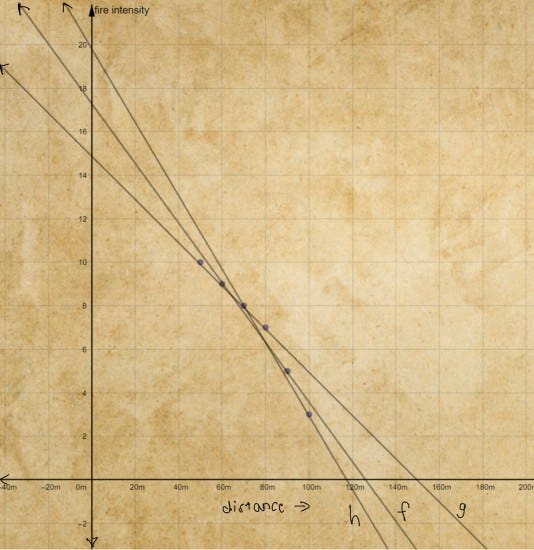
He drew 3 lines. and measured their slopes and y-intercepts looking at the graph.
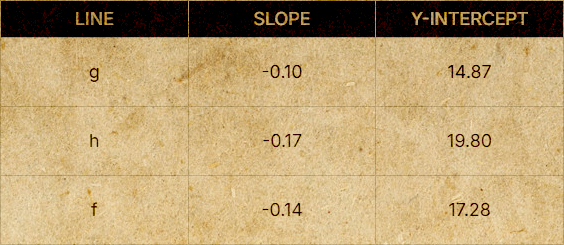
He then substituted these values into the line equation y = mx + c to get the predicted fire intensity for all six distances he had recorded.
Next, for each line, he calculated the errors by taking the absolute difference between the actual fire intensity and the predicted value.
Finally, he added up the errors for each line to see which one had the smallest total — the line that would make his spell the most accurate.

After reviewing his calculations, Peter decided to choose line f. It had the smallest total error among the three.
Now he was ready to face the dragon.
He etched the values of its slope and intercept into his staff and felt the spell settle into place. With his calculations complete, Peter packed his gear and began the climb toward the dragon's mountain.
As he came closer to the dragon's location, the air grew hotter. Molten lava flowed through cracks in the ground. Peter placed each step carefully. Eventually, he reached the location where he had first encountered the dragon.
His heartbeat quickened. His entire body was drenched in sweat from the heat. Doubt crept into his mind. For a moment, he wasn't sure if he should go any further. Fear urged him to turn back.
Peter took a deep breath and forced himself forward.
He walked a few more meters, but there was no sign of the dragon. He scanned every direction, searching for any trace of the beast — but it was nowhere to be seen.
With a mix of disappointment and quiet relief, he decided to retreat and face the dragon another day.
As he turned to leave, he heard a sound — a deep, sudden noise that startled him. He looked in its direction. Far in the distance, he saw the dragon lying still. The noise was its snoring.
"Good lord… it's sleeping. The best time to take it down", Peter thought.
He began moving slowly toward the dragon.
Two hundred meters.
One hundred and fifty.
One hundred.
With each step, the sound grew louder.
Peter activated his staff. The spell came alive, displaying the fire intensity he could expect at each distance. His fear returned. The sight of the dragon so close made his body shiver, but he forced himself onward.
Carefully, he unsheathed his sword, making sure it didn't scrape. This was his chance.

His heartbeat thundered in his ears.
The staff showed 70 meters.
Fire intensity: 7.48.
"If the dragon were awake, I'd be toast at this distance", he thought.
He kept walking. A few steps more.
65 meters.
Fire intensity: 8.18.
Suddenly, the snoring stopped.
A louder sound followed — then a piercing, glowing red light. It took Peter less than a fraction of a second to realize what it was.
The dragon's eye.
The dragon was awake.
"Oh no…oh no", Peter thought.
The dragon locked its gaze onto him and rose to its full height. In an instant, a massive torrent of fire surged toward Peter. Within the flames, glowing fiery symbols — twisted, burning equations — swirled violently, making the attack even more terrifying.
Peter froze. His staff blinked again.
8.18.
The fire struck him. But the intensity wasn't 8.18.
It was a full, unforgiving 10.

(to be continued…)
